그래프

10장 그래프

- 정리의 기반은 학교 강의 노트와 [c언어로 쉽게 풀어쓴 자료구조]를 참고하였습니다.

저의 정리가 옳지 않다면 피드백 부탁드립니다.

---

그래프

• 그래프의 구성 : 정점(vertex) + 간선(edge)의 유한 집합
• 그래프의 표현 : G = (V,E)
• 방향 그래프의 괄호 표현 : <A,B> = A -> B
• 무방향 그래프의 괄호 표현 : (A,B) = A - B
• 네트워크 : 그래프 간선에 가중치 할당 = 가중치 그래프
• 정점의 차수 = 그 정점에 인접한(연결된) 정점의 수
• 무방향 으갤프에서 모든 정점의 차수의 합 = 간선 * 2
• 연결 그래프 : 모든 정점에 항상 경로가 존재하는 그래프
• 완전 그래프 : 모든 정점이 서로 연결되어 있는 그래프

그래프의 표현 방법

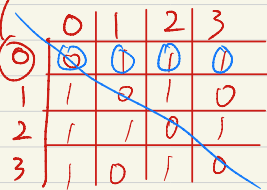
• 인접 행렬 : 2차원 배열

  • 
  • 밀집 그래프 표현에 적합
  • why? n^2의 행렬 저장공간이 애초에 필요하기 때문에
  • 이 행렬은 대칭이므로 상위나 하위 삼각형 배열만 저장하여 메모리를 절약할 수 있다.
  • 간선의 존재 여부 파악 O(1)
  • 정점의 차수 O(n)
  • 모든 간선의 수 O(n^2)

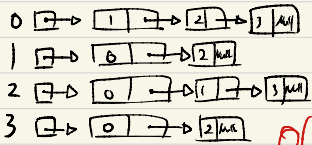
• 인접 리스트 : 연결 리스트

  • 
  • 희소 그래프 표현에 적합
  • 간선의 존재 여부 파악 O(degree(V))
  • 정점의 차수 O(degree(V))
  • 모든 간선의 수 O(n+e)

---

그래프의 탐색

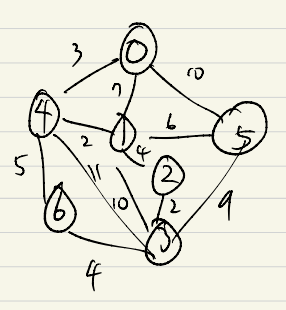
1. 깊이 우선 탐색(Depth First Search)

• 스택 사용
• 인접리스트일 경우 탐색 시간 복잡도 : O(n+e)
• 인접 행렬의 경우 탐색 시간 복잡도 : O(n^2)
• 위 그림에서, 4번째 실행 이후 다시 되돌아가면서 탐색하지만 전부 이미 방문된 노드들이므로 종료.

2. 너비 우선 탐색(Breath First Search)

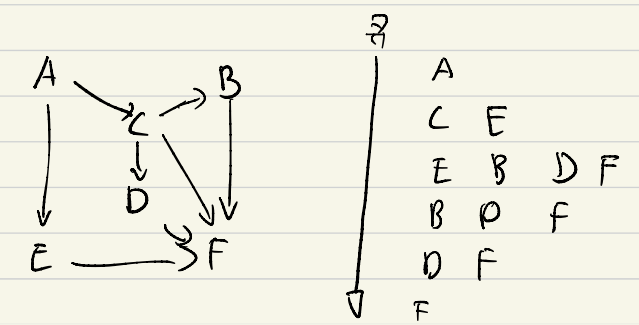
• 큐 사용
• 인접리스트일 경우 탐색 시간 복잡도 : O(n+e)
• 인접 행렬의 경우 탐색 시간 복잡도 : O(n^2)

신장 트리(Spaning Tree)

• 정의 : 그래프 내의 모든 정점을 포함하는 트리
• n개의 정점을 n-1개의 간선으로 연결
• DFS나 BFS 도중에 사용된 간선만 모으면 만들 수 있다.
• 최소 연결 부분 그래프

최소 비용 신장 트리(Minimum Spanning Tree)

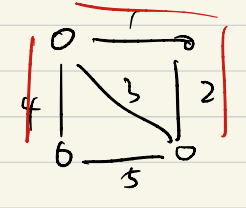
• 정의 : 네트워크를 가장 적은 간선과 비용으로 연결

Kruskal 알고리즘

• Greedy 알고리즘(탐욕)
• 간선들의 가중치를 오름차순으로 정렬
• 이 순서대로 선택(사이클을 형성할 경우 skip)
• 희소 그래프에 적합

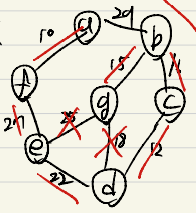
1. 정렬 : 10 12 15 16 18 22 25 27 29
2. 사이클 체크하면서 선택

   Union-find 연산으로 판별

• 이 알고리즘의 시간 복잡도는 간선 정렬 시간에 좌우된다.
  

  • 효율적인 정렬일 경우 : O(

    e

    log

    e

    )

  • 로그의 밑 : 2(로그 표현이 안되서 이렇게 적어둡니다..ㅎ)

Prim 알고리즘

• 시작 정점에서부터 출발하여 신장 트리의 집합을 단계적으로 확장

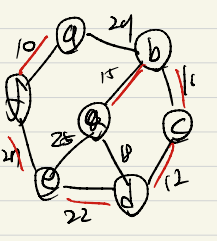
1. 시작점은 아무거나 잡는데 여기서는 a로.
2. a -> f -> e -> d -> c -> b -> g

• O(n^2)의 시간 복잡도
• 밀집그래프에 적합

Dijkstra 최단 경로

• 정의 : 네트워크에서 하나의 시작 정점으로부터 모든 다른 정점까지의 최단 경로를 찾는 것
• 주 반복문을 n번, 내부 반복문을 2n번
• 시간 복잡도 : O(n^2)
• 모든 정점으로부터 최단 경로를 구할 경우 : O(n^2) * n
  
  

Floyd 최단 경로

• 정의 : 모든 정점 사이의 최단 경로
• 2차원 배열을 이용하며, 3중 반복문을 통해 구한다.

글이 길어져서 일단 정의만 서술하고 마무리하겠습니다!