문제
다음과 같은 graph가 주어졌을 때, 출발 vertex 0번부터 시작하여 나머지 모든 vertex까지의 shortest path의 길이(length 또는 cost 또는 weight)를 출력하는 프로그램
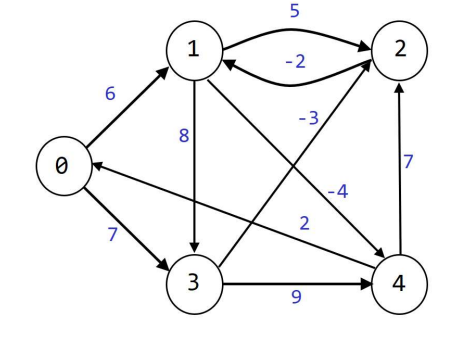
- Bellman-Ford Algorithm 사용
- Adjacency matrix이용
- 출발 정점 : 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<limits.h>
#define INF 10000
//최단경로 값 저장 배열
int dist[101];
//간선
struct Edge
{
int start, end, weight;
};
//그래프
struct Graph
{
int v, e;
struct Edge* edge;
};
//그래프 생성
struct Graph* init(int v, int e)
{
struct Graph* g = (struct Graph*)malloc(sizeof(struct Graph));
g->v = v;
g->e = e;
g->edge = (struct Edge*)malloc((g->e) * sizeof(struct Edge));
return g;
}
void BellmanFord(struct Graph* graph, int start)
{
int v = graph->v;
int e = graph->e;
//일단 시작점부터 모든 VERTEX와의 거리를 무한대로 지정
for (int i = 0; i < v; i++)
{
dist[i] = INF;
}
dist[start] = 0; //시작점부터 시작점까지의 최단 거리는 0
for (int i = 1; i <= v - 1; i++)
{
for (int j = 0; j < e; j++)
{
int u = graph->edge[j].start;
int v = graph->edge[j].end;
int weight = graph->edge[j].weight;
if (dist[u] != INF && dist[u] + weight < dist[v])
//모든 경우의 수에서
//시작점까지의 최단 거리 + 가중치가 도착점의 가중치보다 작을 때
dist[v] = dist[u] + weight; //값 수정
}
}
return;
}
int main(void)
{
int v = 5;
int e = 9;
struct Graph* g = init(v, e);
//그래프 초기화
g->edge[0].start = 0;
g->edge[0].end = 1;
g->edge[0].weight = 6;
g->edge[1].start = 0;
g->edge[1].end = 3;
g->edge[1].weight = 7;
g->edge[2].start = 1;
g->edge[2].end = 2;
g->edge[2].weight = 5;
g->edge[3].start = 1;
g->edge[3].end = 4;
g->edge[3].weight = -4;
g->edge[4].start = 0;
g->edge[4].end = 1;
g->edge[4].weight = 6;
g->edge[4].start = 2;
g->edge[4].end = 1;
g->edge[4].weight = -2;
g->edge[5].start = 3;
g->edge[5].end = 2;
g->edge[5].weight = -3;
g->edge[6].start = 3;
g->edge[6].end = 4;
g->edge[6].weight = 9;
g->edge[7].start = 4;
g->edge[7].end = 0;
g->edge[7].weight = 2;
g->edge[8].start = 4;
g->edge[8].end = 2;
g->edge[8].weight = 7;
//알고리즘 적용
BellmanFord(g, 0);
int n = 0;
printf("도착 vertex를 입력하세요: ");
scanf_s("%d", &n);
printf("\nvertex 0에서 vertex %d으로 가는 최단 경로의 길이는 %d입니다.", n, dist[n]);
return 0;
}
