Krusakl's Algorithm

문제

다음 graph에 대해 minimum cost spanning tree를 생성하는 프로그램을 구현하시오.

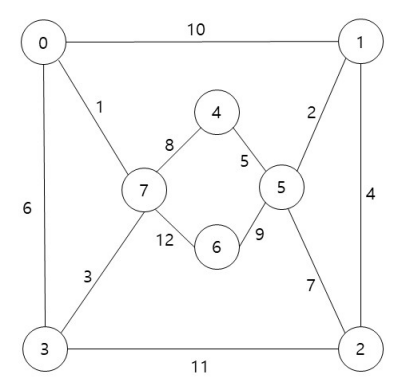
1. Kruskal’s algorithm사용
2. Union, Find 연산 이용
   

---

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0

#define MAX 100

//부모 노드 초기화
int parent[MAX];

//집합 초기화
void set_init(int n)
{	
	//-1로
	for (int i = 0; i < n; i++)
		parent[i] = -1;
}

//x가 속하는 집합 반환
int set_find(int x)
{
	//루트 반환의 경우
	if (parent[x] == -1)
		return x;

    //루트가 아닌 경우 x를 치환하며 루트를 찾는다.
	while (parent[x] != -1) 
		x = parent[x];

	return x;
	
}

//두개의 원소가 속한 집합을 합친다
void set_union(int a, int b)
{
    //a와 b의 루트를 찾는다.
	int root1 = set_find(a);
	int root2 = set_find(b);

	//합침
	if (root1 != root2)
		parent[root1] = root2;
}
//간선 구조체
typedef struct Edge {
	int start, end, weight;
} Edge;

//그래프 구조체
typedef struct GraphType {
	int n;
	struct Edge edges[2 * MAX];
} GraphType;

//그래프 초기화
void graph_init(GraphType* g)
{
	g->n = 0;
	for (int i = 0; i < 2 * MAX; i++) {
		g->edges[i].start = 0;
		g->edges[i].end = 0;
		g->edges[i].weight = 1000; //연결되지 않았으므로 임의의 큰 수 1000을 대입
	}
}

//그래그에 삽입
void insert(GraphType* g, int start, int end, int w)
{
	g->edges[g->n].start = start;
	g->edges[g->n].end = end;
	g->edges[g->n].weight = w;
	g->n++;
}

//qsort()를 사용하기 위한 파라미터 함수
int compare(const void* a, const void* b)
{
	struct Edge* x = (struct Edge*) a;
	struct Edge* y = (struct Edge*) b;
	return (x->weight - y->weight);
}

//kruskal 알고리즘
void kruskal(GraphType* g)
{
	int choose = 0; //현재까지 선택된 간선의 수
	int uset, vset; // 정점 u와 점점 v의 집합 번호
	struct Edge e;

	set_init(g->n); //그래프 초기화
	qsort(g->edges, g->n, sizeof(struct Edge), compare); //간선 가중치 정렬

	printf("kruskal's algorithm을 이용한 minimum cost spanning tree 생성 : ");
	printf("T={ ");

	for (int i = 0; i < (g->n) -1; i++) //간선의 수 < (n-1)
	{
		e = g->edges[i];
		uset = set_find(e.start); //정점 u의 집합 번호
		vset = set_find(e.end); //정점 v의 집합 번호
		
		//서로 속한 집합이 다르면
		if (uset != vset) {
			printf("(%d, %d) ", e.start, e.end);
			choose++;
			set_union(uset, vset); //합침
		}
	}
	printf("}\n\n");
}

int main(void)
{
	GraphType* g;
	g = (GraphType*)malloc(sizeof(GraphType));
	graph_init(g); //그래프 초기화

	//문제에 제시된 대로 삽입
	insert(g, 0, 1, 10);
	insert(g, 0, 3, 6);
	insert(g, 0, 7, 1);
	insert(g, 1, 2, 4);
	insert(g, 1, 5, 2);
	insert(g, 2, 3, 11);
	insert(g, 2, 5, 7);
	insert(g, 3, 7, 3);
	insert(g, 4, 5, 5);
	insert(g, 4, 7, 8);
	insert(g, 5, 6, 9);
	insert(g, 6, 7, 12);
	
	kruskal(g);
	free(g);
	return 0;
}