해싱

13장 해싱

- 정리의 기반은 학교 강의 노트와 [c언어로 쉽게 풀어쓴 자료구조]를 참고하였습니다.

저의 정리가 옳지 않다면 피드백 부탁드립니다.

---

해싱

• 정의 : 키에 산술적인 연산을 적용하여 항목이 저장되어 있는 테이블의 주소를 계산하여 항목에 접근하는 방법
• 탐색 시간 : O(n)

---

해싱 함수의 종류

• 제산 함수(mod) : 나머지 연산
  
  • h(k) = k mod M
  • 위 함수 결과 값의 범위 : 0 ~ M-1
  • M = 주로 소수 사용
    
    
• 폴딩 함수 : 키 > 해시 테이블의 크기일 때 사용
  
  • ex) 32bit / 16bit
  • 키를 몇 개 부분으로 나누어 이를 더하거나 비트별로 부울 연산을 하는것
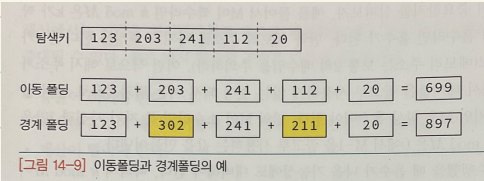
  • 1 : 이동 폴딩 : 키를 여러 부분으로 나눈 값들을 더하여 해시 주소로 사용
  • 2 : 경계 폴딩 : 키의 이웃한 부분을 거꾸로 더하여 해시 주소를 얻음

  
  
  

• 중간 제곱 함수 : 키를 제곱한 다음, 중간의 몇 비트를 취해서 해시 주소 생성, 비교적 고르게 분산
  
  
• 비트 추출 방법 : 해시 테이블 크기가 M=2^k일 때 키를 이진수로 간주하여 임의의 위치 k개의 비트를 해시주소로 사용
  
  • 간단함
  • 해시 주소 집중 현상 가능성 농후

• 숫자 분석 방법 : 각각의 위치에 있는 수의 특징을 미리 알고 있을 때 유용, 편중되지 않는 수들을 해시 테이블의 크기에 적합한 만큼 조합하여 해시 주소로 사용
  • ex) 학번(202212345) 일 때 12345를 주소로 사용

---

충돌

• 정의 : 서로 다른 키를 갖는 항목들이 같은 해시 주소를 가지는 현상
• 충돌이 발생하고 해시 주소에 빈 버킷이 없을 경우 => 오버 플로우 발생
  
  • 해결 방법

    1: 개방 주소법 : 충돌이 일어난 항목을 해시 테이블의 다른 위치에 저장
    2: 체이닝 : 해시 테이블의 하나의 위치가 여러개의 항목을 저장할 수 있도록 구조 변경

개방 주소법 종류

1. 선형 조사법 : 충돌이 ht[k]에서 발생했을 경우, ht[k+1]에서 찾아본다.
   
   • ht[k+1]이 빈 공간이 아닐 경우, ht[k+2]로 가서 찾아본다.
   • 위를 빈공간이 나올 때까지 계속한다.
   • 계속 찾다가 테이블의 끝에 도달할 경우, 테이블 처음으로 가서 찾기 시작한다.

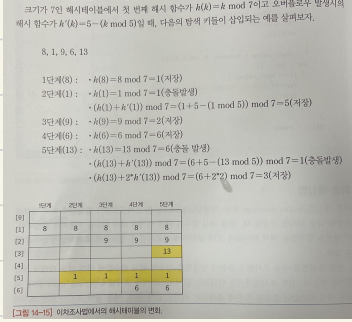
1. 이차 조사법 : 다음 조사할 위치를 식에 의하여 결정
   
   • (h(k) + inc * inc)) mod M for inc = 0, 1, … , M-1
   • 즉, h(k), h(k)+1, h(k)+4, h(k)+9, … mod M
   • 모든 위치를 조사하게 하려면 테이블의 크기가 소수여야 한다.
     
     
2. 이중 해싱법 : 오버플로우가 발생함에 따라 항목을 저장할 다음 위치를 결정할 때, 원래 해시 함수와 다른 별개의 해시 함수를 이용하는 방법
   
   • 해시 테이블의 크기가 반드시 소수여야 한다.

---

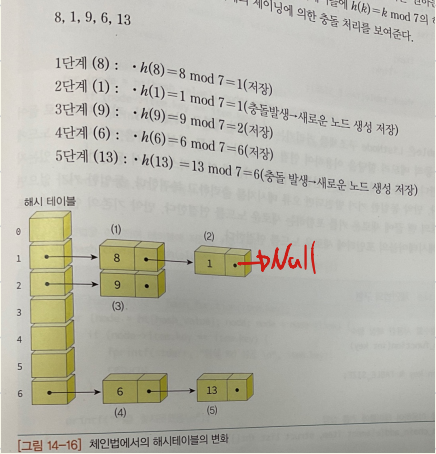
체이닝

• 정의 : 오버플로우를 연결리스트로 해결
• 각 버킷이 연결리스트이다.

해싱 성능

• 해싱에서 가장 중요한 연산은 탐색이다.
• 해시 테이블의 적재 밀도 = 적재 비율 = a = 저장된 항목 갯수 / 해시테이블 버킷 개수 = n / M
• a가 0일 경우 해시테이블은 비어있는 것
• 1일 경우 가득 참
• 체이닝의 경우, a의 최댓값은 없다.
• a가 0.5 이상일 수록 실패한 탐색은 급격하게 탐색 시간 증가