정렬

11장 정렬

- 정리의 기반은 학교 강의 노트와 [c언어로 쉽게 풀어쓴 자료구조]를 참고하였습니다.

저의 정리가 옳지 않다면 피드백 부탁드립니다.
모든 로그의 밑은 2입니다.(수식 표현이 미숙해서…ㅎ)

---

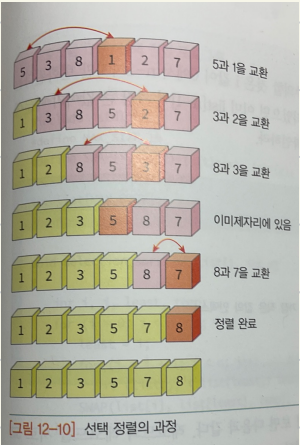
선택 정렬

• 리스트를 왼쪽 리스트(정렬 완료)와 오른쪽 리스트(정렬 미완료)로 나눈다.
• 오른쪽 리스트가 빌 때 까지 가장 작은 수를 선택하여 리스트에 넣는다.
  
  
  
• 장점 : 자료의 이동 횟수가 미리 결정
• 단점 : 안정성이 부족하고, 데이터의 이동 횟수가 많음

---

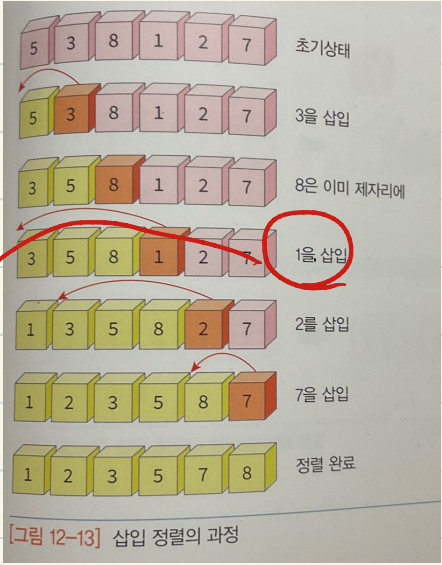
삽입 정렬

• 정렬되어 있는 리스트에 새로운 자료를 적절한 위치에 삽입(정렬되지 않은 부분이 빌 때까지)
• 입력 자료가 이미 정렬되어 있을 경우, 가장 빠르다
• 입력 자료가 역순일 때 최악
• 비교적 이동 횟수가 크다
• 안정성 좋음
  (1 삽입하는 과정을 자세히)
  

---

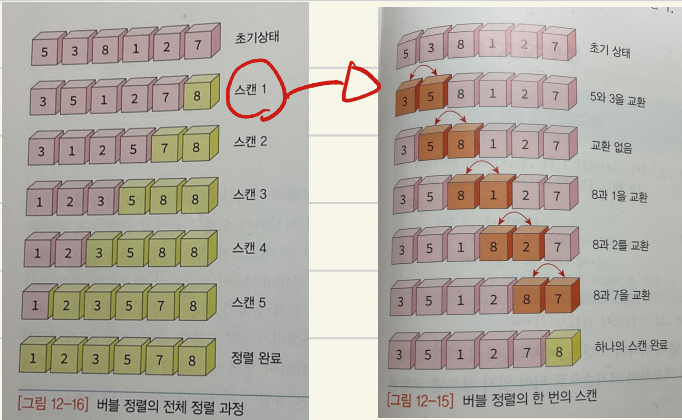
버블 정렬

• 인접한 2개의 레코드를 비교하여 서로 교환(리스트 왼쪽에서 오른쪽 끝까지)
• 어떠한 경우에도 O(n^2)
• 문제점 : 순서에 맞지 않는 요소를 인접한 요소와 교환 -> 특히, 특정 요소가 최종 정렬 위치에 있더라도 교환되는 일이 발생
  

---

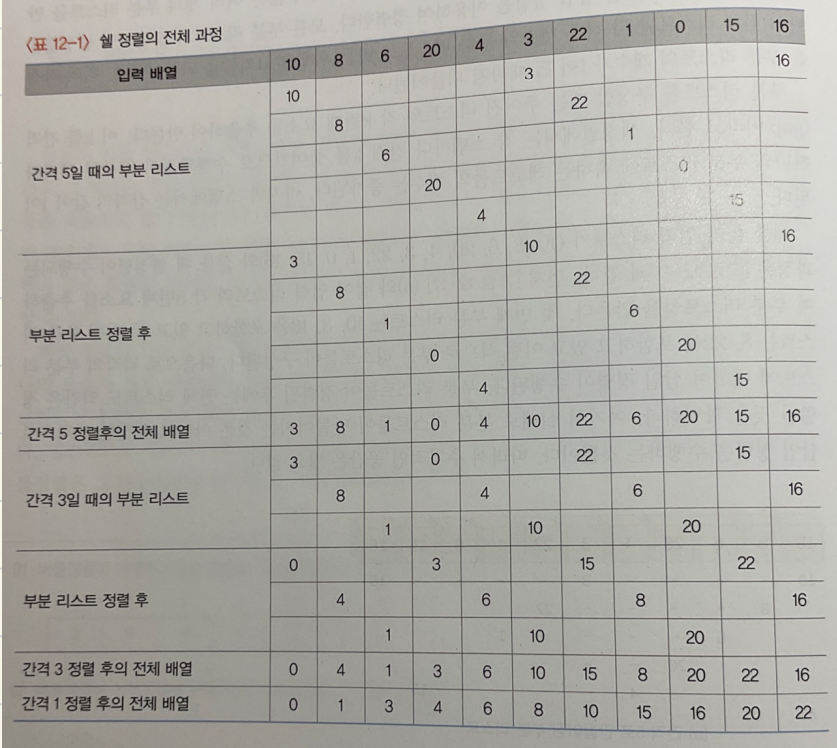
쉘 정렬

• 삽입 정렬이 어느정도 정렬된 배열에서는 대단히 빠르다는 것에서 착안한 방법
• 리스트를 일정한 기준에 따라 분류하여 연속적이지 않은 여러 개의 부분 리스트를 만들고, 각 부분 리스트에 삽입정렬을 이용
• 모든 부분 리스트가 정렬되면, 더 적은 개수의 부분 리스트로 만든 후에 위 알고리즘을 되풀이(부분 리스트의 개수가 1이 될 때까지)
• 최악의 경우 : O(n^2)
• 평균의 경우 : O(n^1.5)
  

---

합병 정렬

• 하나의 리스트를 두개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트를 얻고자 하는 것
• 분할 정복 기법을 바탕
• 모든 경우 : O(nlog n)
• 안정적이고, 데이터 분포에도 영향을 덜 받는다.
  

---

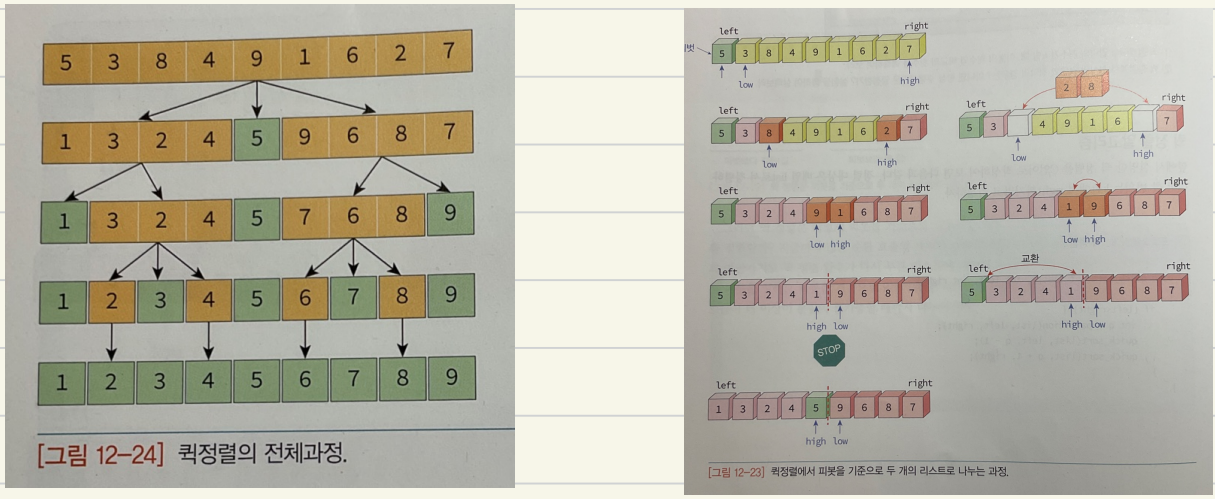
퀵 정렬

• 평균적으로 매우 빠른 수행 속도
• 분할 정복을 바탕
• 합병 정렬과 비슷하게 전체 리스트를 2개의 부분 리스트로 분할하고, 각각의 부분 리스트를 다시 퀵 정렬
• 피벗을 선택한 후, 피벗보다 작으면 왼쪽, 크면 오른쪽으로 이동
• 이 상태에서 피벗을 제외한 왼쪽, 오른쪽 리스트를 다시 정렬(순환 호출)
• 평균의 경우 : O(nlog n), 그 중에서도 가장 빠름
• 최악의 경우 : O(n^2)
• 단점 : 정렬된 리스트일 경우, 오히려 시간이 더 오래 걸린다.
  

---

히프 정렬

• 배열을 최소 히프로 변환 후, 가장 작은 원소부터 추출하여 정렬
• O(nlog n)
  

---

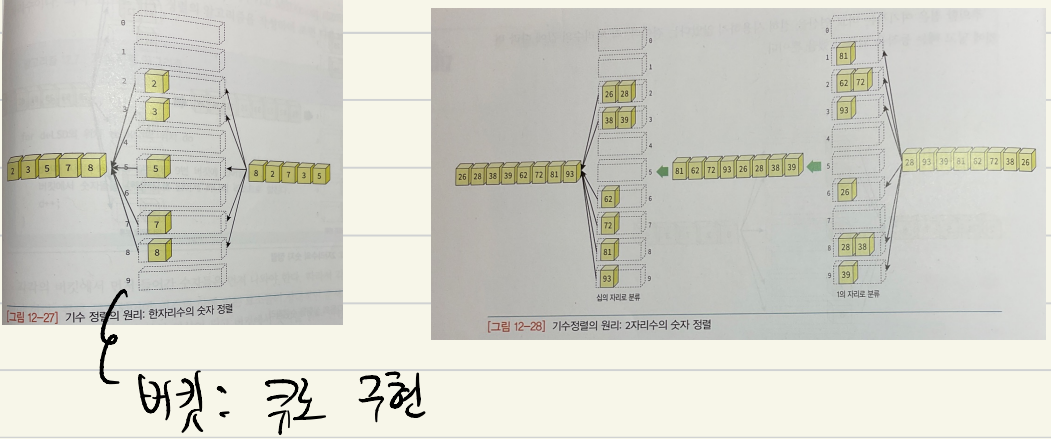
기수 정렬

• 데이터를 서로 비교하지 않고 정렬
• 정렬의 이론적 하한선인 O(n log n)을 깨는 유일한 방법
• O(kn) (k <= 4)
• 단점
  • 메모리 추가 사용
  • 정렬할 레코드의 타입이 한정적
  • 레코드의 키들이 동일한 길이여야한다.

---

정렬 방법의 성능 비교

알고리즘	최선	평균	최악
삽입 정렬	O(n)	O(n^2)	O(n^2)
선택 정렬	O(n^2)	O(n^2)	O(n^2)
버블 정렬	O(n^2)	O(n^2)	O(n^2)
쉘 정렬	O(n)	O(n^1.5)	O(n^2)
퀵 정렬	O(nlog n)	O(nlog n)	O(n^2)
히프 정렬	O(nlog n)	O(nlog n)	O(nlog n)
합병 정렬	O(nlog n)	O(nlog n)	O(nlog n)
기수 정렬	O(dn)	O(dn)	O(dn)