백준 1456번(거의 소수)[JAVA]

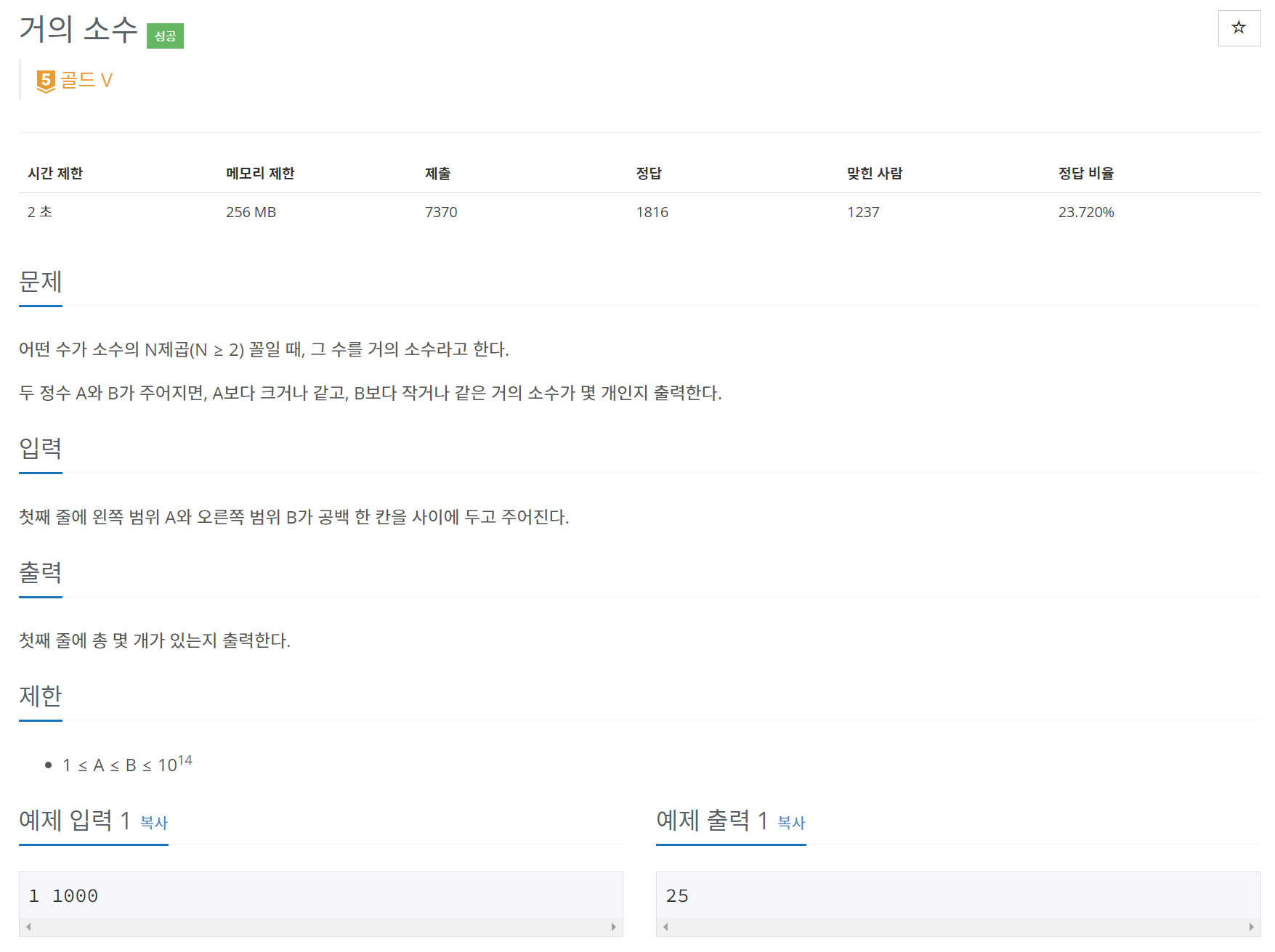
풀이

에라토스테네스의 체를 이용하여 푼다.

1. 범위가 1~B까지인 배열 생성
2. 1은 소수가 아니므로 0으로 대체
3. 2를 제외한 2의 배수 모두 0으로 대체
4. 지워지지 않은 다음 수가 3이므로, 3을 제외한 3의 배수 모두 0으로 대체
5. 위 과정을 n의 제곱근까지 반복
6. 0이 아닌 값들을 제곱하여 B보다 작으면 cnt++

팁
수의 최대가 10^14승이므로 long으로 선언
cnt변수로 개수를 셀 때, 제곱한 값이 long범위를 초과할 수 있으므로 각 변을 제곱근으로 나눠서 비교한다.

소스 코드

import java.util.*;

public class 거의소수 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		long a = sc.nextLong();
		long b = sc.nextLong();
		long[] arr = new long[10000001];
		
		for (int i = 2; i < arr.length ; i++) {
			arr[i] = i;
		}
		
		for (int i = 2; i < Math.sqrt(arr.length); i++) {
			if (arr[i] == 0)
				continue;
			
			for (int j = i+i; j < arr.length; j=j+i) {
				arr[j] = 0;
			}
		}
		int cnt = 0;
		for (int i = 2; i < arr.length; i++) {
			if (arr[i] != 0) {
				long tmp = arr[i];
				while (true) {
					if ((double)arr[i] > (double)b/(double)tmp)
						break;
					if ((double)arr[i] >= (double)a/(double)tmp)
						cnt++;
					tmp = tmp * arr[i];
				}
			}
		}
		System.out.println(cnt);
	}
}

태클 감사합니다.
조언 환영입니다.